WORKSHOP
Mathematical Justification for the Kinetic and Fluid Equations of Plasmas and Self-Gravitating Systems
Justification mathématique des équations cinétiques et fluides des plasmas et systèmes autogravitants
24 – 28 July, 2023
Scientific Committee
Comité scientifique
Julien Devriendt (Oxford University)
Isabelle Gallagher (ENS – PSL)
Pierre Emmanuel Jabin (PennState University)
Laure Saint-Raymond (IHES)
Local Organizing Committee
Comité d’organisation local
Nicolas Besse (Observatoire de la Côte d’Azur)
Stéphane Colombi (CNRS Institut d’Astrophysique de Paris)
Yves Elskens (Aix-Marseille Université)
Roland Triay (Aix-Marseille Université)
A primary objective, when studying a complex physical system from a theoretical perspective, is to describe it as simply as possible. With N-body systems such as plasmas, dark matter in the Universe, or even stars in galaxies, the first step in the simplification procedure often amounts to calculating kinetic limits at large N. More specifically, it involves showing that a system with a large number N of particles can be described by a kinetic equation governing the evolution of a one (or possibly two) particle distribution function when N tends to infinity, as, for example, the Boltzmann equation. In a second step, one can further simplify the kinetic equation by focusing on the evolution of the first moments of the distribution function. For instance, only considering the first two velocity moments, the Boltzmann equation can be reduced to the Navier-Stokes equations for hydrodynamics, provided the mean free path between two collisions is small compared to the size of the system. Thirdly, under the assumption that specific parameters remain small, a simplified (perturbative) approach to the resolution of the equations of motion makes it possible to reduce the problem to wave-particle interactions or wave-wave interactions. In cosmology for example, perturbation theory is widely used to precisely constrain models of large scale structure formation in the Universe.
The passage to the different limits, kinetic, fluid, or even the justification of the use of perturbation theory remains, because of the associated inherent difficulties and subtleties, the subject of intense discussions between mathematicians and physicists. The purpose of this multidisciplinary workshop is to review and critically evaluate the latest developments on specific aspects of these problems, with a particular emphasis on their mathematical justification.
Un objectif primordial lors de l’étude théorique d’un système physique complexe est de décrire ce dernier le plus simplement possible. Dans les systèmes N-corps comme les plasmas, la matière noire dans l’Univers, ou encore les étoiles dans les galaxies, la première étape fondamentale de cette procédure de réduction revient souvent à calculer des limites cinétiques à N grand. Il s’agit dans ce cas de montrer qu’un système avec un grand nombre N de particules peut être décrit par une équation cinétique régissant l’évolution d’une fonction de distribution à une (voire deux) particule lorsque N tend vers l’infini, par exemple l’équation de Boltzmann. On peut même dans un deuxième temps simplifier encore plus les équations en ne se concentrant que sur l’évolution des premiers moments de la fonction de distribution. Par exemple, l’équation de Boltzmann peut se réduire aux équations de Navier-Stokes lorsque le libre parcours moyen entre deux collisions est petit devant la taille du système. Dans un troisième temps, en supposant que certains paramètres adimensionnés sont petits, une approche (perturbative) simplifiée de la résolution des équations du mouvement permet alors de réduire le problème à des interactions onde-particule ou des interactions onde-onde. En cosmologie, par exemple, la théorie des perturbations est largement utilisée pour contraindre avec précision des modèles de formation des grandes structures de l’Univers.
Le passage aux différentes limites, cinétiques, fluides, ou encore la justification de l’emploi de théories des perturbations restent encore l’objet, à cause de leur difficulté et de leur subtilité, de discussions entre mathématiciens et physiciens. L’objet de ce workshop pluridisciplinaire est de passer en revue et d’évaluer de manière critique les derniers développements sur certains aspects spécifiques de ces problèmes en mettant l’accent sur la justification mathématique.
Detailed scope
Kinetic and fluid equations provide important insights in plasma physics and gravitational dynamics, and pose important problems in analysis and numerical analysis. This workshop will focus on the articulation between these descriptions.
Kinetic limits in the context of Hamiltonian or diffusive/dissipative dynamics
This involves showing that a system composed of a large number N of particles, governed by a distribution function (BBGKY hierarchy) or an empirical measure in phase-space, can be described by a kinetic equation with a one-particle distribution function (even also sometimes with one- and two-particle distribution functions coupled together) when N tends to infinity. These particle systems can be Hamiltonian or dissipative/diffusive. For Hamiltonian systems, one can mention the kinetic limit of a system subjected to the Coulomb or Newtonian force towards the Vlasov-Poisson equation. In astrophysics, one can think about stars in galaxies or dark matter in the Universe. For diffusive systems, one can cite the kinetic limit of particles subjected to billiard dynamics (ballistic transport plus elastic shocks) to the classical collisional Boltzmann equation. One can also mention other more complex kinetic limits such as that towards the Balescu-Lenard-Guernsey equation.
Fluid limits
It is a question of showing that in certain physical regimes where some dimension-free parameters become small, a kinetic equation can be approximated by fluid equations on the moments of the distribution function in velocity space. In the dissipative case, one can quote the approximation of the collisional Boltzmann equation by the Navier-Stokes equations when the mean free path between two collisions is small compared to the size of the system (or small Knudsen number). In the Hamiltonian case, one can, for example, cite the Vlasov-Poisson fluid limit to the incompressible Euler equations in the quasi-neutral limit.
Approximate models and applications
The collective behavior in these models gives rise to waves, which can also be considered as dynamic actors. Wave-particle and wave-wave interactions are physico-mathematical mechanisms at the base of many crucial approximate models in physics. For example, for the linear wave-particle interaction, when the phase velocity of a wave is close to the velocity of a particle, the quasi-linear approximation of the Vlasov equation accounts for the saturation of electromagnetic instabilities by a velocity diffusion equation on the spatial mean of the distribution function. Concerning the wave-wave interaction, one can quote weak turbulence, which makes it possible to predict the behavior of the wave spectrum in fluid mechanics by modelling the transfer of energy between large and small scales due to the coupling of waves produced by non-linear terms. Analogous approaches allow one to predict the evolution of the power-spectrum of the large-scale matter distribution in the Universe with higher order cosmological perturbation theory. In quantum mechanics, one can also think about the approximation of the Schrödinger equation by a kinetic equation of waves of the collisional Boltzmann type. Finally, propagation of chaos is a cross-cutting theme to the previous ones. In this case, it is a question of proving that, if a system of particles initially satisfies certain statistical properties (e.g., independence), then they are conserved over time by the dynamics, justifying certain reduced descriptions.
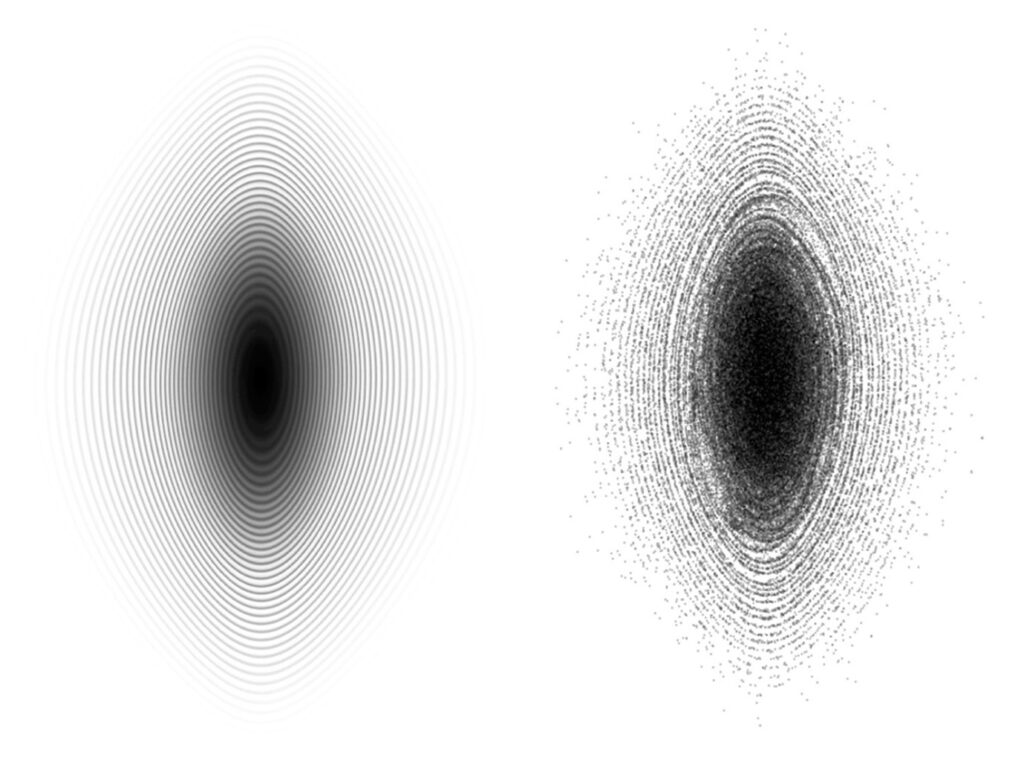
Convergence to the Vlasov solution: N-body versus Vlasov simulations in 1D gravity. On the left, the “exact” evolved state of an initially Gaussian distribution function in phase space, with a Vlasov solver, on the right, the result obtained with a N-body code. The finite-N solution is subject to instabilities that disappear in the mean field limit. Images realized by S. Colombi, C. Alard and J. Touma (www.vlasix.org).
SPEAKERS
Claude Bardos (Sorbonne Université) Homogenous Approximations for solutions of the Vlasov Equation from Quasi Linear to Balescu Lenhard equation
Julien Barré (Université d’Orléans) Hydrodynamic limits, macroscopic fluctuations and large deviations
Nicolas Besse (Observatoire de la Côte d’Azur) Welcome address
Pierre-Henri Chavanis (CNRS Université Toulouse III Paul Sabatier) A heuristic wave equation parameterizing BEC dark matter halos with a quantum core and an isothermal atmosphere
Charles Collot (CY Cergy Paris Université) On the derivation of the kinetic wave equation of wave turbulence
Stéphane Colombi (CNRS, Institut d’Astrophysique de Paris) The early evolution of cosmic structures
Sten Delos (Max Planck Institute for Astrophysics) Prompt cusp formation from the cosmological initial conditions
Julien Devriendt (University of Oxford) On the ability of quadrature-based moment methods to follow cold dark matter dynamics
Mitia Duerinckx (Université Libre de Bruxelles) Dynamics of point-vortex systems around equilibrium
Dominique Escande (CNRS, Aix-Marseille Université) The Vlasovian limit: a singular and renormalized description of the actual N-body dynamics
Manuela Feistl (University of Tübingen) Microscopic Derivation of Vlasov type equations
Ouassim Feliachi (Université d’Orléans) Dynamical large deviations for homogeneous system with long-range interactions
Jean-Baptiste Fouvry (CNRS Institut d’Astrophysique de Paris) Kinetic theory of one-dimensional long-range interacting N-body systems at order 1/N^2
Guido Giachetti (CY Cergy Paris Université) Coarse-grained collisionless dynamics with long-range interactions
François Golse (École Polytechnique) The Regularity Problem for the Landau Equation
Michael Kiessling (Rutgers University) On the microscopic foundations of the relativistic Vlasov-Maxwell equations
Philip-J. Morrison (The University of Texas at Austin) The metriplectic 4-bracket: a curvature-like framework for describing dissipation in joined Hamiltonian and dissipative fluid and plasma systems
Clément Mouhot (University of Cambridge) Review of recent mathematical progresses on Landau damping without confinement
Yann Munschy (CEA Cadarache) Kinetic plasma-wall interaction using immersed boundary conditions
Alessia Nota (University of L’Aquila) Long-time asymptotics for Homoenergetic solutions of the Boltzmann equation
Francesco Pegoraro (University of Pisa) A 1-dimensional electrostatic plasma model for testing the validity of kinetic theory
Cornelius Rampf (University of Vienna) Vlasov–Poisson equations and shell-crossings
Valeria Ricci (University of Palermo) Mathematical modelling of magnetic reconnection
Tarcisio Rocha Filho (University of Brasilia) Analytic Solution of the One-Dimensional Vlasov-Poisson System
Pascal Tremblin (CEA Saclay) Non-ideal self-gravitating hydrodynamics
Roland Triay (Aix-Marseille Université) Round table
Anh-Tuan Vu (Aix-Marseille Université) Long time behavior for collisional strongly magnetized plasma in three space dimensions
Raphael Winter (University of Vienna)
Simon White (Max Planck Institute for Astrophysics) A universal density profile from hierarchical clustering














