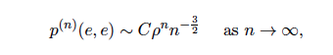Fuchsian groups are an important class of finitely generated hyperbolic groups. Recently there have been signifiant developments in the theory of random walks on these groups – most notably a central limit theorem [3, 2, 11] and a local limit theorem [9, 7] have been established. These breakthroughs have stimulated considerable interest in probability theory on Fuchsian groups, and there are many fundamental and important open questions remaining. In this project we will address two of these questions:

(1) The local limit theorem states that the return probabilities of a random walk behaves as

where C is a constant and p < 1 is the spectral radius of the walk. The spectral radius is one of the most important numerical values associated to the random walk, however to date there are no known explicit formulas for p for non-elementary one-ended hyperbolic groups. In our project we want to develop new techniques and methods to approximate the spectral radius, providing improvements on recent numerical bounds.

(2) The question studied involves the analysis of excursions of the random walk. More precisely,
we want to prove that long excursions of the random walk converge after suitable time and
space rescaling to the Brownian continuum random tree.